Pirámide (base cuadrada) - área y volumen
Calculadora en línea — introduce los valores y obtén el resultado al instante, con la fórmula y un ejemplo.
A = área
V = volumen
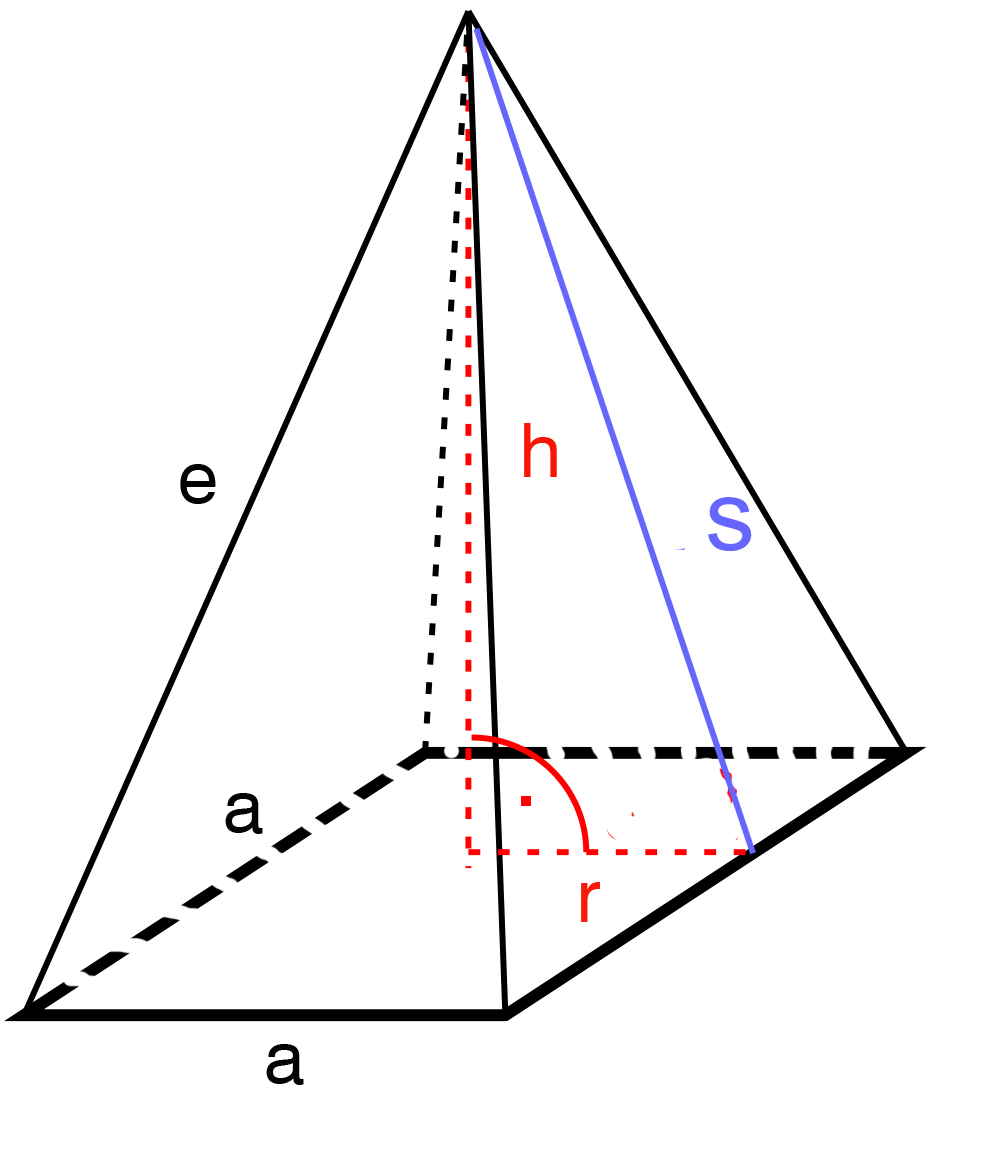
a = lado "a"
h = altura
s = altura inclinada del triángulo
BA = área de la base
LA = área lateral
Una pirámide de base cuadrada es un cuerpo tridimensional cuya base es un cuadrado y cuyas cuatro caras triangulares se elevan desde las aristas de la base hasta encontrarse en un único punto llamado ápice. Tiene, por tanto, 5 caras, 8 aristas y 5 vértices, y cuando el ápice se sitúa justo encima del centro del cuadrado se denomina pirámide recta, que es perfectamente simétrica. En este cuerpo importan dos alturas: la altura vertical, medida en línea recta desde el centro de la base hasta el ápice, y la apotema, medida a lo largo de una cara triangular desde el ápice hasta el punto medio de una arista de la base. Su volumen es igual a un tercio del área de la base multiplicada por la altura vertical, de modo que una pirámide siempre contiene un tercio del prisma que comparte su misma base y altura. Su área superficial es la suma de la base cuadrada y las cuatro caras triangulares idénticas. Las pirámides de base cuadrada aparecen a lo largo de la arquitectura y la historia, sobre todo en las pirámides de Egipto, y todavía se emplean hoy en tejados, monumentos y el diseño de envases.
Volumen de la pirámide V
–
Área superficial S
–
Altura de la cara vs
–
| Área de la base SZ | – |
| Superficie lateral SP | – |
Arrastra una esquina de la base (a) o el vértice (v) Centrar
Ejemplo resuelto
El lado de la base de la pirámide es 4 cm y la altura de la pirámide es 6 cm. Calculemos el área y el volumen de la pirámide.
Área de la superficie de la pirámide:
Primero calculamos el área de la base como SB = a * a = 4 * 4 = 16 cm²
Para calcular el área lateral necesitamos la apotema (altura inclinada), que calculamos usando el teorema de Pitágoras c² = a² + b². En lugar de a² usamos (a/2)², así 4/2 = 2, y en lugar de b² usamos la altura 6. Entonces c² = 2² + 6² = 40
c = √40 = 6.32.
La altura inclinada es entonces 6.32 cm.
El área lateral se calcula como SL = 4 * ((a * s) / 2) = 4 * ((4 * 6.32) / 2) = 50.56 cm²
El área total de la pirámide es la suma de la base y el área lateral, es decir, 16 + 50.56 = 66.56 cm²
Volumen de la pirámide:
Usando la fórmula V = (SB * v) / 3, sustituimos los valores: V = (16 * 6) / 3 = 32 cm³
