Pyramid (square based) - area and volume
A = SB+SL
BA = a*a
LA = 4*((a*s)/2)*4
V=(SB*v)/3
A = Area
V = volume
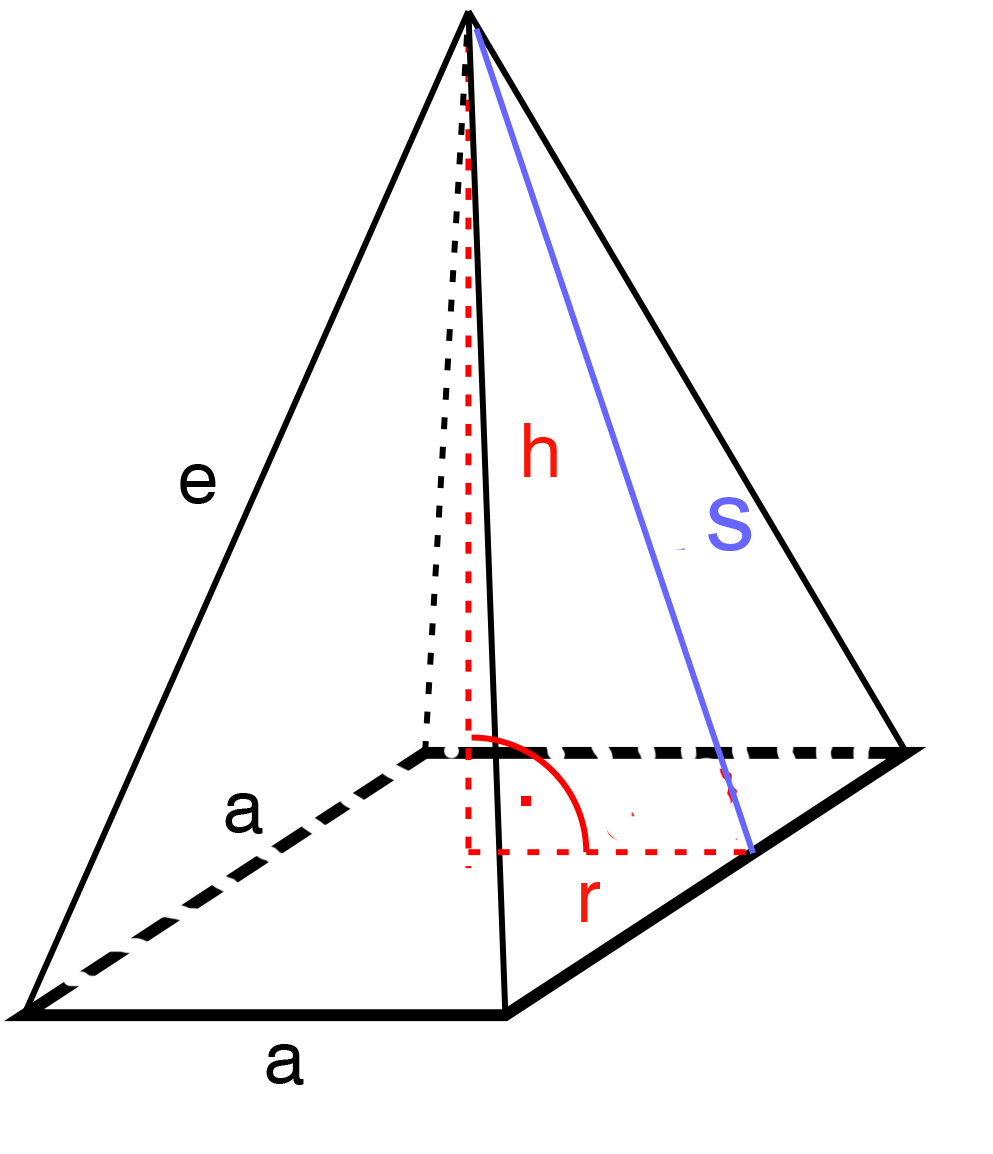
a = side "a"
h = height
s = slant triangle height
BA = basement area
LA = lateral area
WHAT IS IT ?
A square-based pyramid is a three-dimensional geometric shape with a square base and four triangular faces that converge at a single point called the apex. The properties of a square-based pyramid include:
- Base: A square with four equal sides.
- Apex: The single vertex where all triangular faces meet.
- Height (h): The perpendicular distance from the center of the base to the apex.
- Slant Height: The distance from the apex to the midpoint of any side of the base.
The surface area of a square-based pyramid is the sum of the area of the square base and the areas of the four triangular faces. The volume of a square-based pyramid is one-third the product of the base area and the height. Square-based pyramids are commonly found in various applications in mathematics, architecture (such as the pyramids of Egypt), and design.
CALCULATION:
EXAMPLE:
The side of the base of the pyramid is 4 cm, the height of the pyramid is 6 cm. Let's calculate the area and volume of the pyramid.
Surface area of the pyramid:
First, we calculate the area of the base as SC = a * a = 4 * 4 = 16 cm²
To calculate the lateral area, we need the slant height, which we calculate using the Pythagorean theorem c² = a² + b². Instead of a², we use (a/2)², so 4/2 = 2, and instead of b², we use the height 6. Then c² = 2² + 6² = 40
c = √40 = 6.32.
The slant height is thus 6.32 cm.
The lateral area is then calculated as SC = 4 * ((a * s) / 2) = 4 * ((4 * 6.32) / 2) = 50.56 cm²
The total area of the pyramid is then the sum of the base and the lateral area, thus 16 + 50.56 = 66.56 cm²
Volume of the pyramid:
Using the formula V = (SZ * v) / 3, we substitute the values V = (16 * 6) / 3 = 32 cm³
