Cotangent
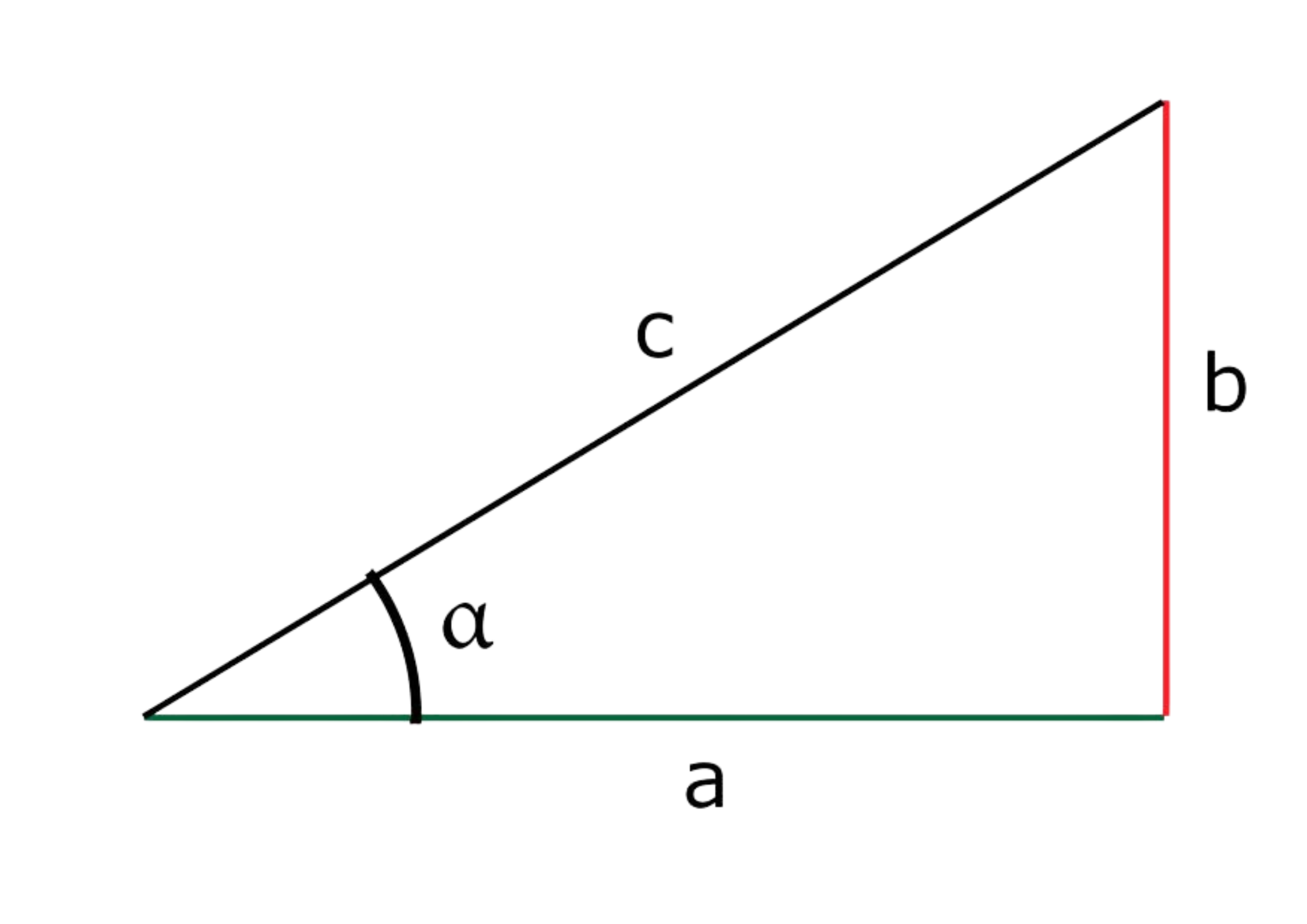
cot alpha α = a/b
α = angle alpha
a = side "a"
b = side "b"
c = side "c"
WHAT IS IT ?
The cotangent of an angle (cot) is the ratio of the length of the adjacent side to the opposite side.
CALCULATION:
EXAMPLE:
Let's assume we have a right triangle ABC, where ∠C=90o. Side a is adjacent to angle α, side b is opposite to angle α, and c is the hypotenuse (the longest side of the triangle).
The definition of the cotangent of angle α is:
The cotangent of an angle (cot) is the ratio of the length of the adjacent side to the opposite side.
For this example:
cot α = a/b
Example:
Assume the side lengths are:
- a = 3
- b = 4
- c = 5
- Verify that the triangle is right-angled using the Pythagorean theorem:
a2 + b2 = c2
32 + 42 = 52
9 + 16 = 25
Since the equality holds, it is a right triangle.
2. Calculate the cotangent of angle α:
cot α = a/b = 3/4 = 0.75
Result:
cot α = 0.75
Thus, the cotangent of angle α in this right triangle is 0.75.
YOU MIGHT BE INTERESTED:
COMMENTS:
