O = 2πr. α / 360°
S=(πr2*360/α) - obsah trojuholníka
O = obvod
S = obsah
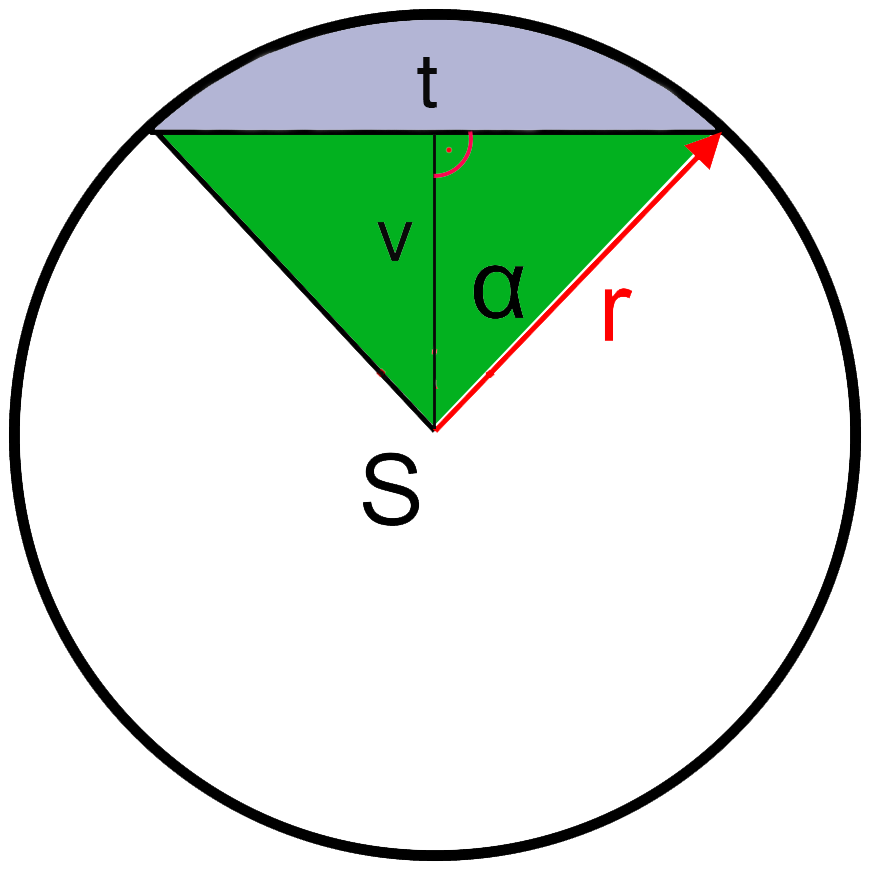
S = stred
α = uhol
r = polomer
t = dĺžka tetivy

O = 2πr. α / 360°
S=(πr2*360/α) - obsah trojuholníka
O = obvod
S = obsah
S = stred
α = uhol
r = polomer
t = dĺžka tetivy
Polomer kruhu je 5 cm, uhol α je 60 stupňov
Pri výpočte musíme najprv vypočítať kruhový výsek a to ako S=(πr2*α)/360 teda
S= (3,14*5 na 2*60)/360 = (3,14*25*60)/360 = 13,08 cm2
Teda obsah kruhového výseku je 13,08 cm2.
Aby sme dalej mohli vypočítať obsah kruhového odseku musíme od kruhového výseku odpočítať obsah trojuholníka.
Obsah trojuholníka vypočítame pomocou sínusu uhla podľa ktorého je sínus uhla pomer protiľahlej odvesny a prepony. Preponou je v našom prípade polomer a uhlom pre potreby sinusu je 1/2 uhla α teda 30 stupňov.
Takže
sin 30 stuňov = (1/2 tetivy) / prepona (polomer)
0,5 = (1/2 tetivy) / 5
0,5 * 5 = (1/2 tetivy)
2,5 cm = (1/2 tetivy) teda celá tetiva je 5 cm
Výšku v vypočítame podla Pytagorovej vety
c2 = a2 + b2
5 na druhu (polomer) = 2,5 na druhú + b2
25 =6,25 + b2
18,75 = b2
4,33 = b teda výška v
Trojuholník vypočítame podla vzorca
S = (a * v) / 2
S = (5 * 4,33) / 2
S = 10,82
Obsah kruhového odseku sa potom rovná obsah kruhového výseku - obsah trojuholníka teda 13,08 - 10,82 teda 2,21 cm2
Obvod kruhového odseku vypočítame pomocou vzorca
O = 2πr. α / 360°
O = (2*3,14*60)/360
O = 5,24 cm